POMDP Planning

Partially observable Markov decision processes (POMDPs) can be used to model a wide range of real world problems from robotics, to games, to critical resource projects necessary for the green transition. Although studied since the 1960s, scalability of POMDP solvers is still a major challenge. Offline solvers often use some form of value iteration to compute optimal policies over a (limited) discrete set of states. They can handle long time horizons but don’t scale well to larger problems, especially those with continuous states actions and observations. Online solvers often employ forward tree search from a root belief and can naturally scale to high dimensional problems, as well as incorporate non-Markov constraints. Their drawback is that they are typically limited to a shorter planning horizon due to the exponential expansion of the search tree. Since we primarily work on very large POMDPs, we have recently focused on improving forward-search methods.

BetaZero: Combining Planning and Learning for Solving POMDPs

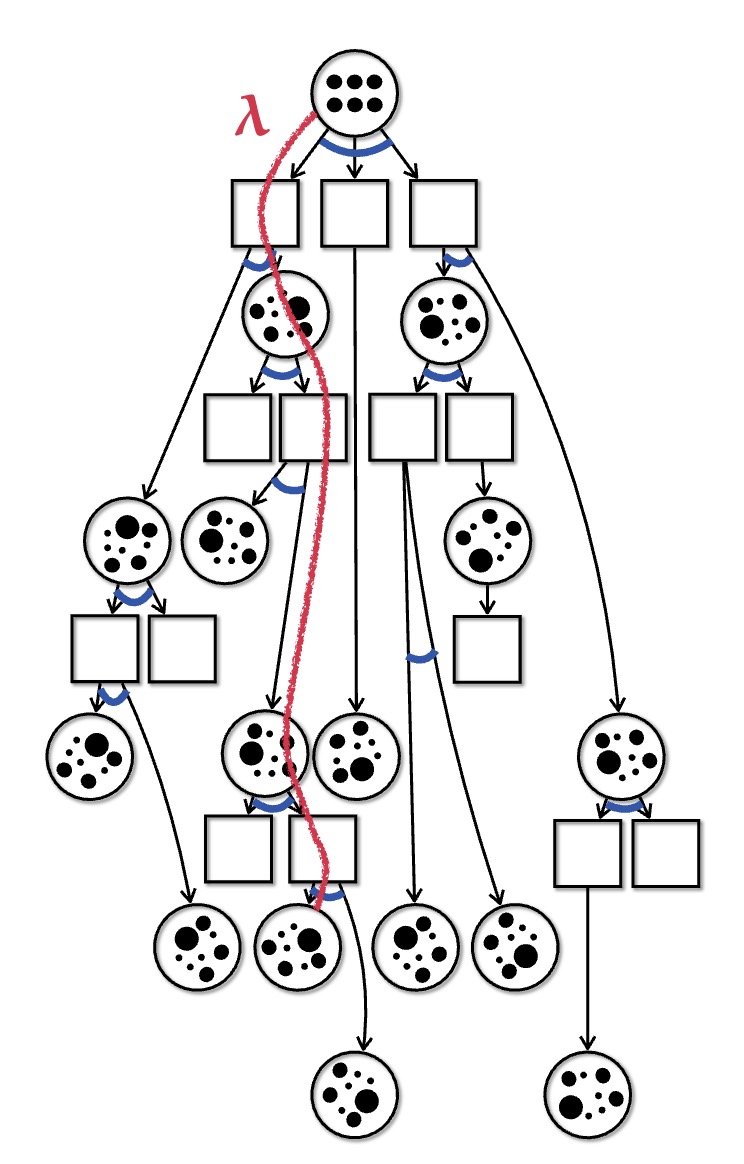
The key insight of our recent paper, is that reinforcement learning can be used to estimate the value of unexplored states in a tree search. The insight is an extension of the popular AlphaZero algorithm to the partially observed setting. The algorithm is depicted below. We first convert the POMDP into a belief-state MDP and use a double progressive widening form of Monte Carlo tree search (MCTS). Then, through repeated interactions with the environment, we learn a value function and an approximately optimal policy from the data. These are used to improve the next round of MCTS planning by using the policy to select new actions and to approximate the value of unexplored states. The process is repeated until the performance of the algorithm converges. Check out the code here.

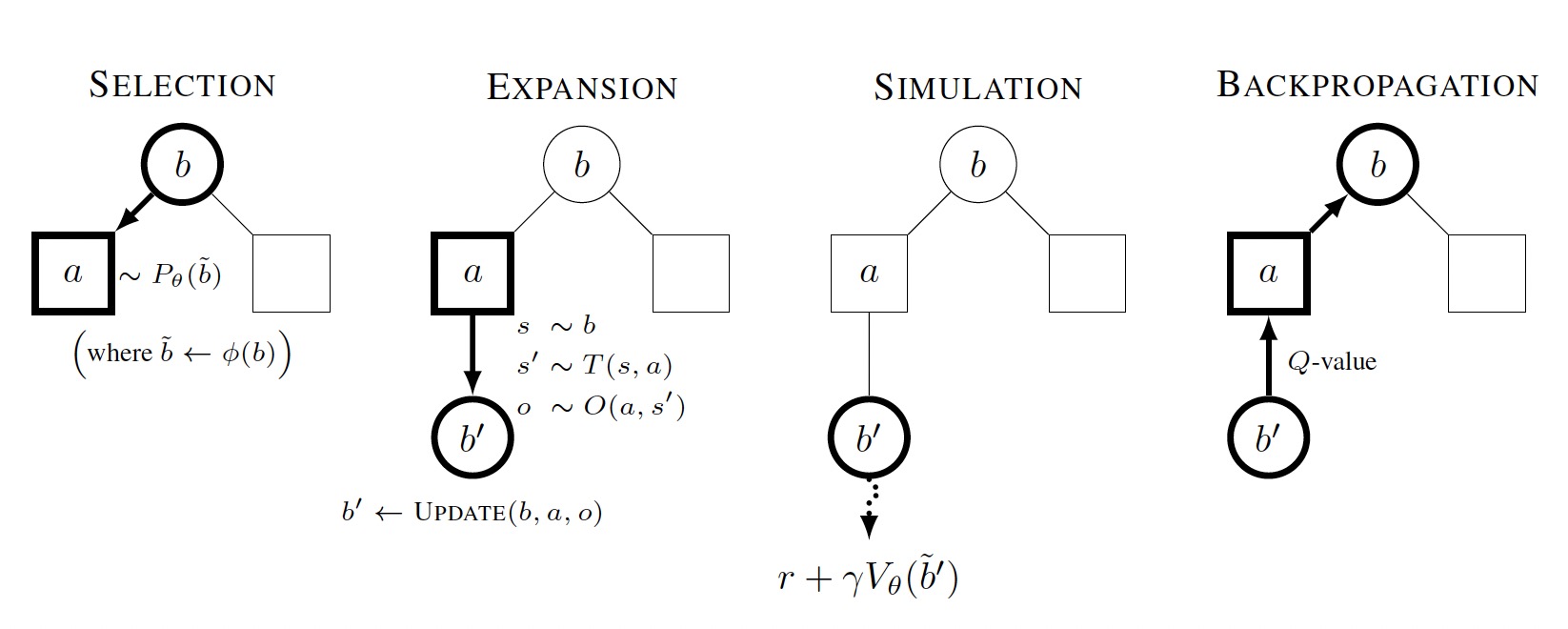
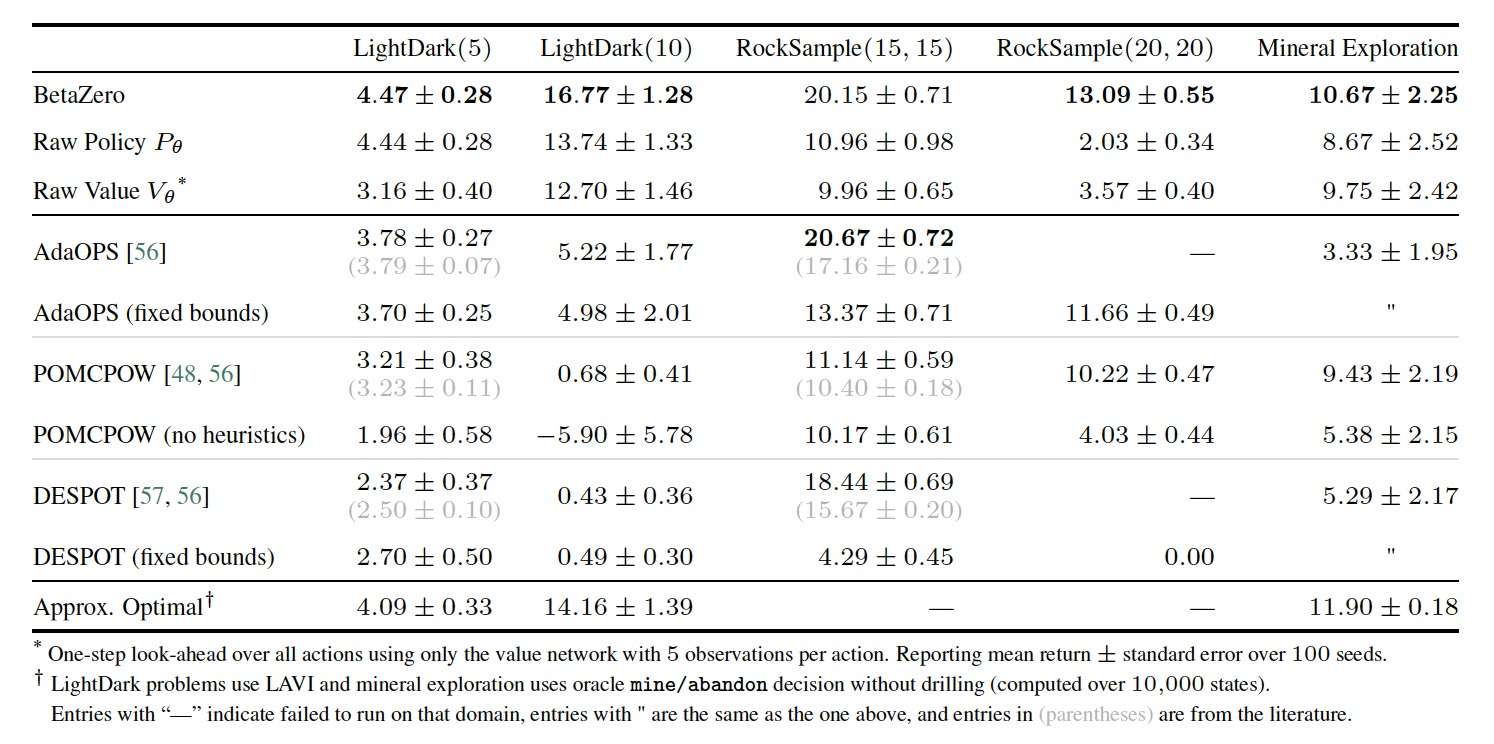
Below is a comparison to other state of the art POMDP solvers.

Constrained POMDP Planning

When planning in safety-critical settings, it is often preferable to formulate safety requirements as hard constraints on the planner, rather than penalizing violations in the reward function. Our recent paper extends the popular POMCPOW and PFT algorithms to incorporate constraints through dual ascent. The approach is depicted below. The planner maintains a lagrange multiplier parameter that is increased or decreased depending on the expected cost observed in the search tree. The reward is augmented with the lagrange-multipler-scaled cost to ensure constraint satisfaction.

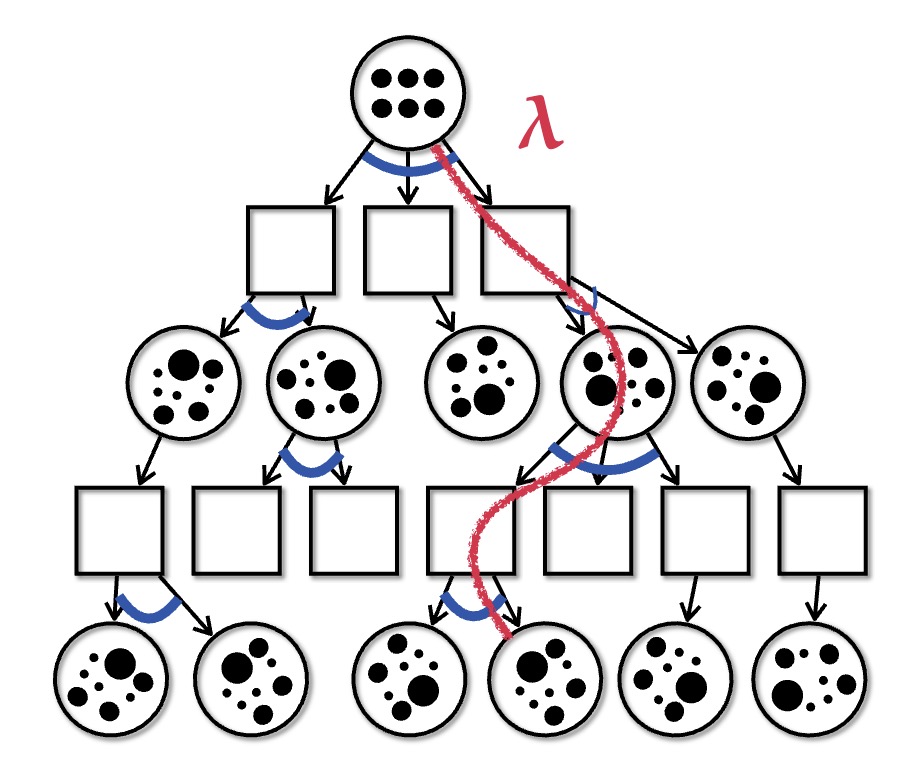
Rather than having to select a penalty parameter a priori, we can instead specify a hard constraint and the planner will maximize the reward subject to that constraint. We compare the approach to a penalty approach with various values of the penalty parameter and show that the constrained planner produces a solution at the pareto-optimal point.

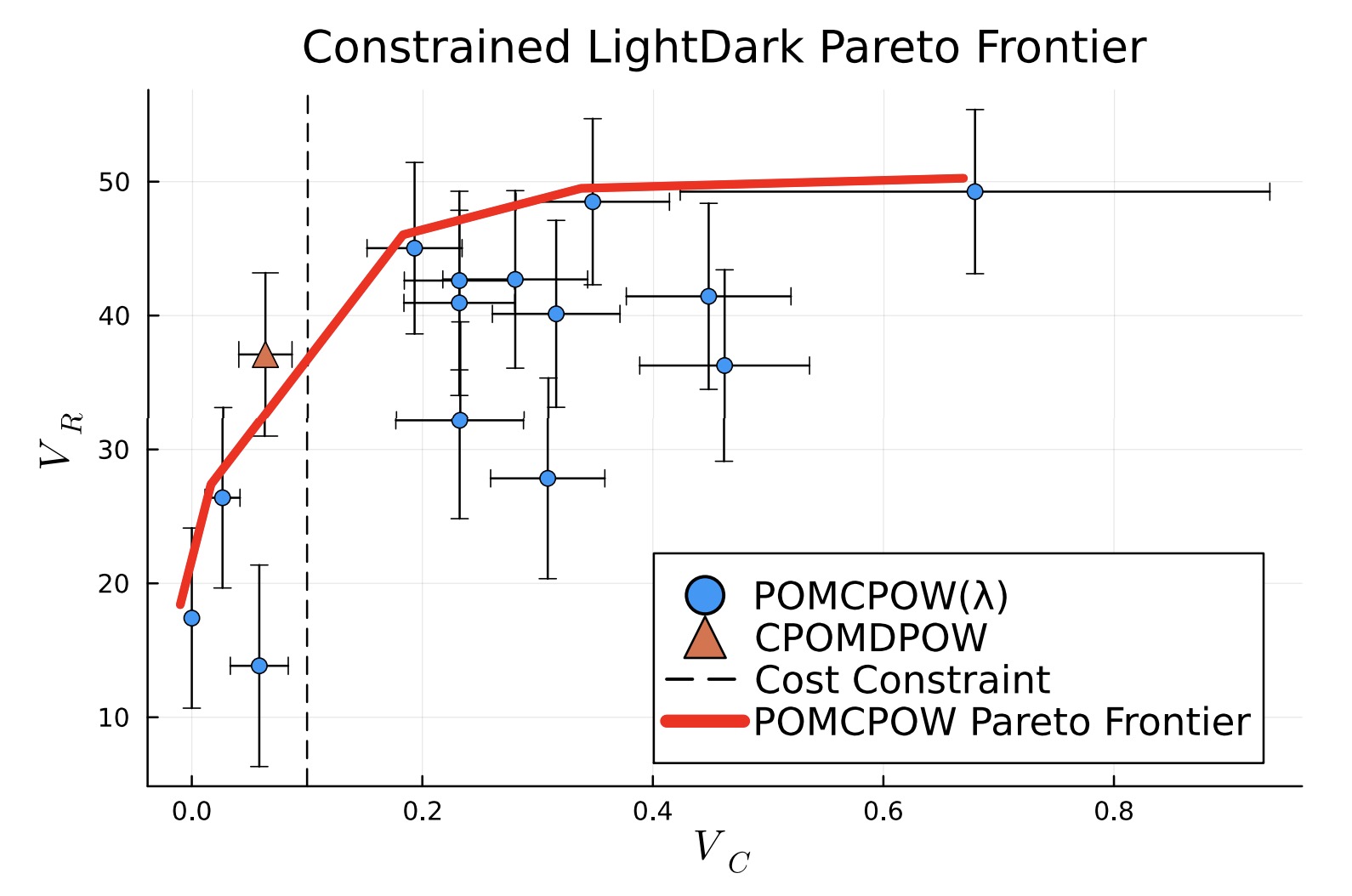
We are currently working on an extension of the algorithm that works with options, allowing us to search over longer planning horizons.

Ongoing Work

We are currently extending the work on POMDP planning a few directions

• Developing value-iteration-based solvers for large POMDPs in order to better handle long time horizons
• Dimensionality reduction of POMDPs using data-driven representation learning
• Incorporating constraints into offline solvers